Settings

Switch modes

Help to visualize

More

Joy of convolution

© Tobias Kaulich

(Discrete Time) Convolution

The behavior of a linear, time-invariant discrete-time system with input signal x[n] and output signal y[n] is described by the convolution sum: The signal h[n], assumed known, is the response of the system to a unit-pulse input.
The convolution summation has a simple graphical interpretation. First, plot h[k] and the "flipped and shifted" x[n - k] on the k axis, where n is fixed. Second, multiply the two signals to obtain a plot of the summand sequence indexed by k. Summing the values of this sequence with respect to k yields y[n]. These operations can be repeated for every value of n of interest.

(Continuous Time) Convolution

The behavior of a linear, continuous-time, time-invariant system with input signal x(t) and output signal y(t) is described by the convolution integral 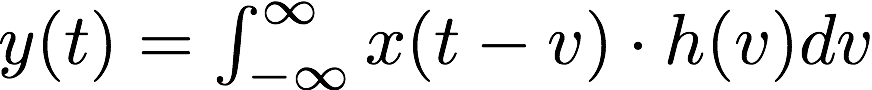The signal h(t), assumed known, is the response of the system to a unit impulse input. To compute the output y(t) at a specified t, first the integrand h(v)x(t - v) is computed as a function of v.Then integration with respect to v is performed, resulting in y(t).
These mathematical operations have simple graphical interpretations.First, plot h(v) and the "flipped and shifted" x(t - v) on the v axis, where t is fixed. Second, multiply the two signals and compute the signed area of the resulting function of v to obtain y(t). These operations can be repeated for every value of t of interest.

Explore graphical convolution


To explore graphical convolution, select signals x[n] or h[n] from the provided examples below, or use the mouse to create your own or modify a signal. Furthmore, by using a right mouse click, one can start drawing polygons between right mouse click events and end them with a single left mouse click.
Click and drag on the the plot displaying x[n-k] and h[k] to modify the current k-value. During dragging the plot of x[n-k] * h[k] as well as the plot of y[n]will be updated live.

x[n] x[t] Your Browser does not support the HTML5-Canvas element.
h[n] h[t] Your Browser does not support the HTML5-Canvas element.
Your Browser does not support the HTML5-Canvas element. Your Browser does not support the HTML5-Canvas element. x[n-k] and h[k] x[t-v] and h[v] Move to right Move to left
x[n-k] times h[k] x[t-v] times h[v] Your Browser does not support the HTML5-Canvas element. Reset y scaling to fit current frame.
y[n] = sum from k = -infinity to infinty for x[n-k] times h[k] y[n] = integrate v from -infinity to infinty for x[t-v] times h[v] Your Browser does not support the HTML5-Canvas element. Reset y values to 0.